P Np Np Complete And Np Hard Problems Pdf
Tractability difference between tractability and intractability can be slight can find shortest path in graph in om nlgn time but finding longest simple path is np complete. By definition there exists a poly time algorithm as that solves x.
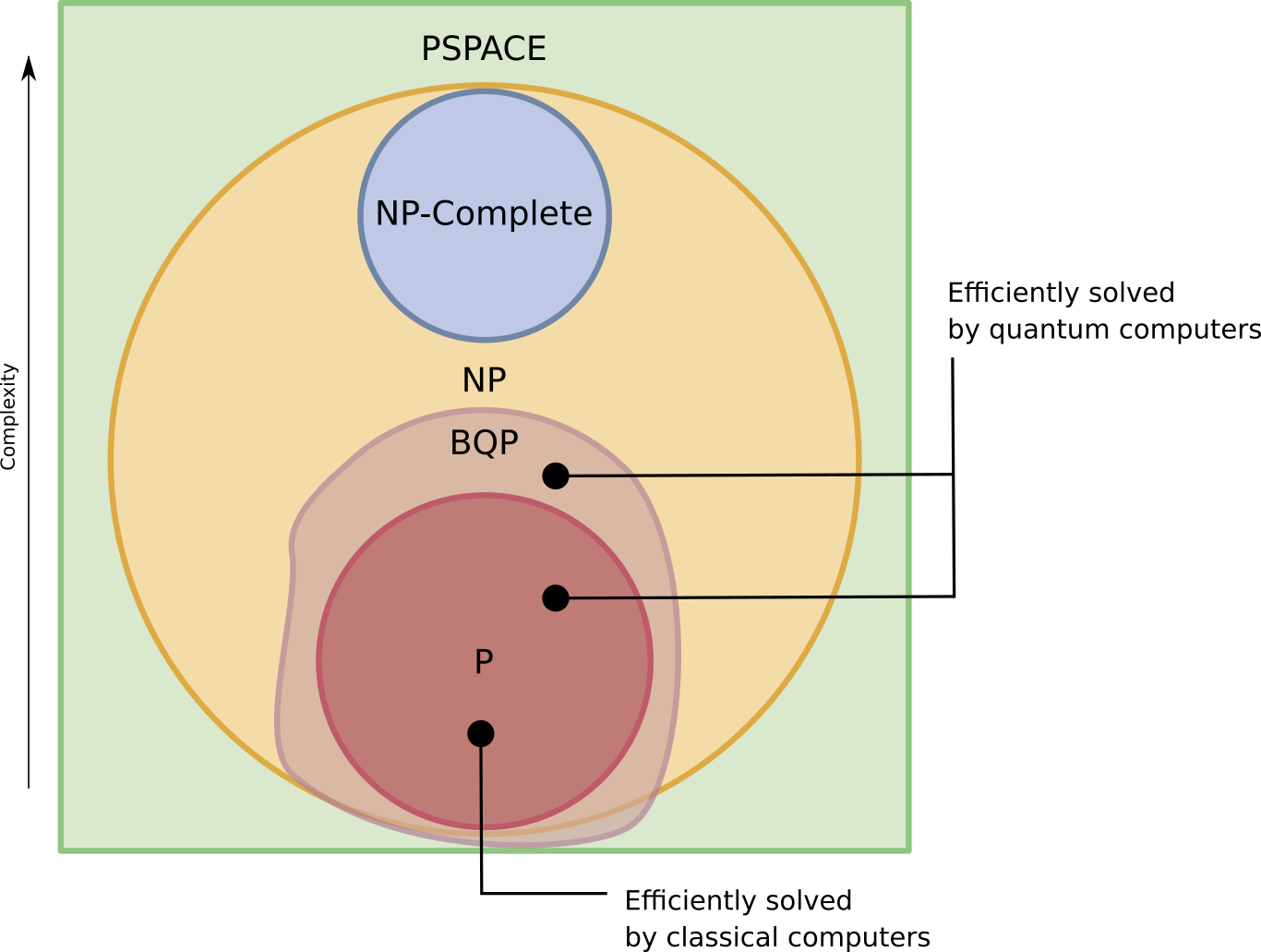
An Update On Quantum Computing And Complexity Classes Quantum Bits
Decision problems for which there is an exponential time algorithm.
P np np complete and np hard problems pdf. Decision problems for which there is a poly time algorithm. The first part of an np completeness proof is showing the problem is in np. The precise definition here is that a problem x is np hard if there is an np complete problem y such that y is reducible to x in polynomial time.
P polynomial time solving. Sometimes we can only show a problem np hard if the problem is in p then p np but the problem may not be in np. Np hardness non deterministic polynomial time hardness is in computational complexity theory the defining property of a class of problems that are informally at least as hard as the hardest problems in npa simple example of an np hard problem is the subset sum problem.
So i thought of explaining them in an easy way. The problem in np hard cannot be solved in polynomial time until p np. Instead we can focus on design approximation.
All np complete problems are np hard but all np hard problems are not np complete. P np and exp p. It might be because of the name but many graduate students find it difficult to understand np problems.
Consider any problem x p. A problem h is np hard when every problem l in np can be reduced in polynomial time. Hard to it eg np complete problem.
The class of np hard problems is very rich in the sense that it contain many problems from a wide. Np hard and np complete problems if an np hard problem can be solved in polynomial time then all np complete problems can be solved in polynomial time. P and np many of us know the difference between them.
A more precise specification is. Problems which can be solved in polynomial time. If a problem is proved to be npc there is no need to waste time on trying to find an efficient algorithm for it.
Note that np hard problems do not have to be in np and they do not have to be decision problems. Np problems have their own significance in programming but the discussion becomes quite hot when we deal with differences between np p np complete and np hard. The second part is giving a reduction from a known np complete problem.
Intuitively these are the problems that are at least as hard as the np complete problems. Np complete problems have no known p time solution considered intractable. Decision problems for which there is a poly time certifier.
Informally a search problem b is np hard if there exists some np complete problem a that turing reduces to b.

Proof That Vertex Cover Is Np Complete Geeksforgeeks

Frontiers Using Stochastic Spiking Neural Networks On Spinnaker
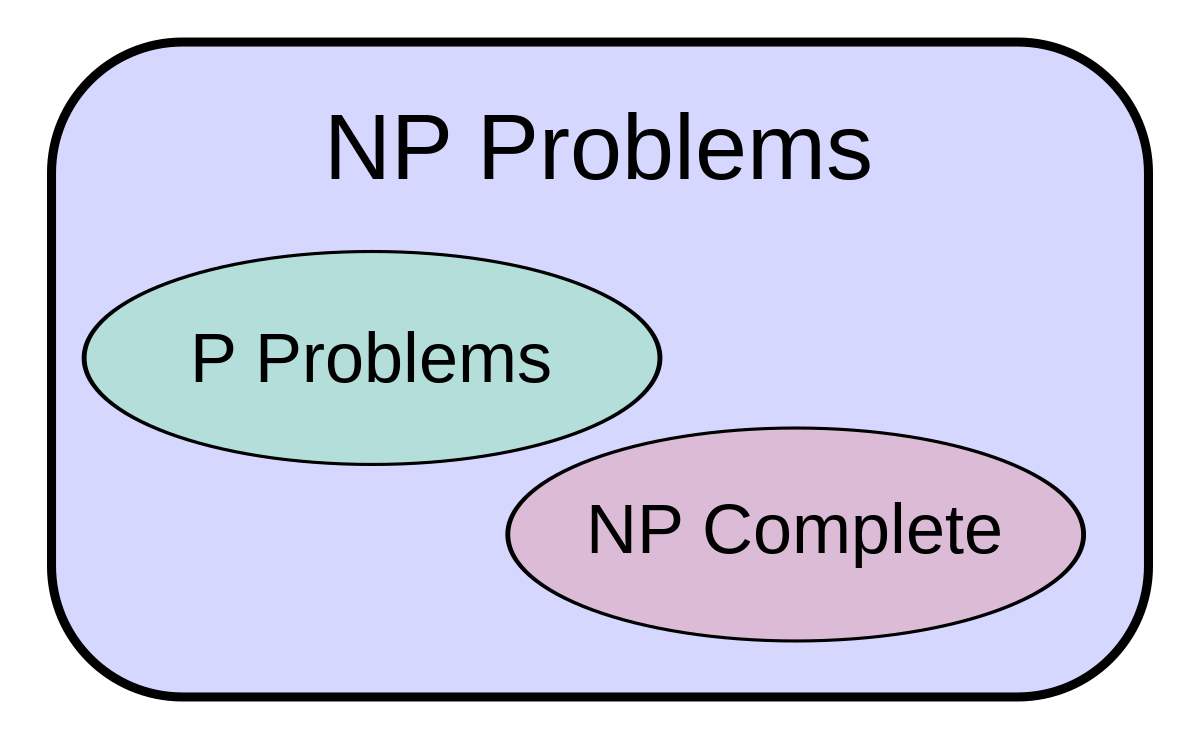
P Versus Np Problem Wikipedia
Complexity Classes Computational Complexity Theory Time Complexity
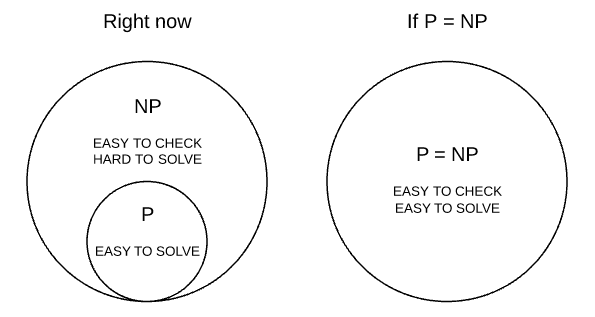
P Vs Np Problem In A Nutshell Bilal Aamir Medium

P Np Np Complete Np Hard Gate Cse

Computational Complexity Of Ecological And Evolutionary Spatial
P Versus Np Problem Wikipedia

Np Completeness Set 1 Introduction Geeksforgeeks
